来源:模型视角
在日常生活中,许多事物都可以使用图和网络来表示。这些事物的关系和相互作用可以通过图论和复杂网络的原理进行分析。在本文中,我们将探讨图论和复杂网络在现代生活中的几个关键应用,并对图论的表示方法和复杂网络的特性进行简要介绍。
1 图论的表示方法
图论是数学的一个分支,主要研究图的性质和图上的运算。一个图 通常表示为 ,其中 是节点集,而 是边集。
- 加权图: 每条边都有一个与其相关的数值,称为权重。
举个例子,你和你的朋友们形成了一个圈子,每个人都是这个圈子中的一个点。如果你和某个朋友关系特别好,那么就可以用一条线连接你们两个点。这就是图论的基础。
如果这条线没有方向(即你和你的朋友都认为彼此是好朋友),那么这就是一个“无向图”。如果这条线有方向(比如说你关注了某位明星,但明星并不认识你),那么这就是一个“有向图”。如果你给这条线加上一个数字,表示你们之间的关系有多好,那么这就是一个“加权图”。
城市的道路就像一个加权的无向图,每个交叉路口是一个点,每条道路是一条线,而道路的长度或者通行时间就是那个数字。
2 复杂网络的性质及数学表达
复杂网络是由大量节点和边组成的网络,具有以下性质:
- 小世界性:网络中任意两个节点之间的平均最短路径较短。
- 无标度性:节点的度分布遵循幂律分布,即少数节点有很高的度,而大多数节点的度较低。
数学上,复杂网络的一些性质可以通过以下参数来描述:
- 平均路径长度 : 所有节点对之间最短路径的平均值。
- 集群系数 : 节点的邻居间存在的边数与可能存在的边数之比的平均值。
3 应用
3.1 交通网络优化
城市的交通网络是一个巨大的复杂系统。通过图论的方法,每个交通节点(如公交站、地铁站)都可以表示为图中的一个点,而路径(如道路、铁轨)则为边。利用图论的算法,如Dijkstra算法、Floyd算法等,我们可以优化交通路径,减少拥堵,为城市居民提供更高效的出行方案。
3.2 社交网络分析
社交网络中的每个个体(用户)都可以被视为一个节点,而他们之间的关系(如朋友、关注者)则形成边。通过复杂网络的方法,我们可以分析网络中的关键节点、社区结构以及信息的传播路径。此外,社交网络分析还可以用于推荐系统,为用户推荐可能感兴趣的内容或朋友。
3.3 电力网格稳定性
电力网格是一个巨大的电力传输网络。每个发电站或变电站都可以视为一个节点,而电线则为边。通过图论和复杂网络的分析,我们可以预测并防止电网故障,确保电力供应的稳定性。
3.4 生态系统网络
在生态系统中,不同的生物种群之间存在食物链和相互作用关系。这些关系可以用复杂网络来表示。通过分析这些网络,我们可以更好地理解生态系统的稳定性和生物多样性。
4 虚拟网络分析
我们构建了一个虚拟的社交网络,使用Erdós-Rényi模型生成了一个随机图(Erdős-Rényi模型 (ER模型) 是随机图理论中的一个经典模型,它是由Paul Erdős和Alfréd Rényi在20世纪60年代独立提出的。ER模型描述了一个随机过程,用来生成随机图)。
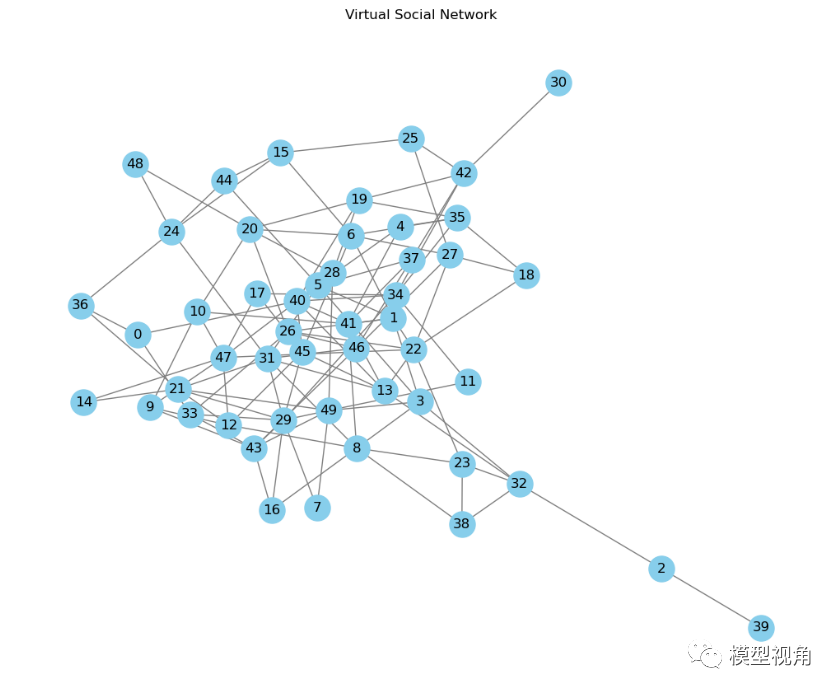
以下是该虚拟社交网络的一些性质:
- 平均度 : 平均每个节点的连接数。在这个的网络中, 。这意味着在这个虚拟社交网络中,平均每个人与约5个其他人有联系。
- 平均聚类系数 : 度量网络中节点之间连接的紧密程度。在该网络中, 。这意味着节点的邻居间平均有 的可能性彼此相连。
- 平均最短路径长度 : 所有节点对之间最短路径的平均值。在我们的网络中, 2.55。这意味着在这个虚拟社交网络中,任意两个人之间的平均“社交距离”约为 2.55 。
从上述性质中,我们可以观察到网络具有较短的平均最短路径长度,这是“小世界”网络特性的体现。同时,平均聚类系数相对较低,这可能意味着这个网络中的个体群体不太紧密。
通过图论工具,我们可以更好地理解和改善我们的日常生活,帮助我们分析和理解现实世界中的复杂系统。通过这些方法,我们可以优化交通、分析社交关系、确保电力供应稳定并更好地保护生态系统。随着技术的进步,这些工具在未来的应用将会更加广泛。 作者:王海华
原文链接:https://mp.weixin.qq.com/s/yJO8UC1WN61AkcPe6MrIQQ